delays = bpd.read_csv('data/united_summer2015.csv')
delays.plot(kind='hist', y='Delay', bins=np.arange(-20.5, 210, 5), density=True, ec='w', figsize=(10, 5), title='Population Distribution of Flight Delays')
plt.xlabel('Delay (minutes)');
# Run this cell to set up packages for lecture.
from lec17_imports import *
Suppose $x$ is a numerical variable, and $x_i$ is one value of that variable. Then, $$x_{i \: \text{(su)}} = \frac{x_i - \text{mean of $x$}}{\text{SD of $x$}}$$
represents $x_i$ in standard units – the number of standard deviations $x_i$ is above the mean.
SAT scores range from 400 to 1600. The distribution of SAT scores has a mean of 1050 and a standard deviation of 200. Your friend tells you that their SAT score, in standard units, is 3.5. What do you conclude?
The distribution of flight delays that we've been looking at is not roughly normal.
delays = bpd.read_csv('data/united_summer2015.csv')
delays.plot(kind='hist', y='Delay', bins=np.arange(-20.5, 210, 5), density=True, ec='w', figsize=(10, 5), title='Population Distribution of Flight Delays')
plt.xlabel('Delay (minutes)');
delays.get('Delay').describe()
count 13825.00
mean 16.66
std 39.48
...
50% 2.00
75% 18.00
max 580.00
Name: Delay, Length: 8, dtype: float64
Since we have access to the population of flight delays, let's remind ourselves what the distribution of the sample mean looks like by drawing samples repeatedly from the population.
sample_means = np.array([])
repetitions = 2000
for i in np.arange(repetitions):
sample = delays.sample(500) # Not bootstrapping!
sample_mean = sample.get('Delay').mean()
sample_means = np.append(sample_means, sample_mean)
sample_means
array([18.31, 14.68, 17.02, ..., 17.74, 14.48, 15.84])
bpd.DataFrame().assign(sample_means=sample_means).plot(kind='hist', density=True, ec='w', alpha=0.65, bins=20, figsize=(10, 5));
plt.scatter([sample_means.mean()], [-0.005], marker='^', color='green', s=250)
plt.axvline(sample_means.mean(), color='green', label=f'mean={np.round(sample_means.mean(), 2)}', linewidth=4)
plt.xlim(5, 30)
plt.ylim(-0.013, 0.26)
plt.title('Distribution of the Sample Mean for Samples of Size 500')
plt.legend();
Notice that this distribution is roughly normal, even though the population distribution was not!
The Central Limit Theorem (CLT) says that the probability distribution of the sum or mean of a large random sample drawn with replacement will be roughly normal, regardless of the distribution of the population from which the sample is drawn.
While the formulas we're about to introduce only work for sample means, it's important to remember that the statement above also holds true for sample sums.
The function sample_mean_delays takes in an integer sample_size, and:
sample_size directly from the population.def sample_mean_delays(sample_size):
sample_means = np.array([])
for i in np.arange(2000):
sample = delays.sample(sample_size)
sample_mean = sample.get('Delay').mean()
sample_means = np.append(sample_means, sample_mean)
return sample_means
Let's call sample_mean_delays on several values of sample_size.
sample_means = {}
sample_sizes = [5, 10, 50, 100, 200, 400, 800, 1600]
for size in sample_sizes:
sample_means[size] = sample_mean_delays(size)
Let's look at the resulting distributions.
plot_many_distributions(sample_sizes, sample_means)
What do you notice? 🤔
# Compute the standard deviation of each distribution.
sds = np.array([])
for size in sample_sizes:
sd = np.std(sample_means[size])
sds = np.append(sds, sd)
sds
array([17.89, 12.92, 5.5 , 3.82, 2.8 , 1.96, 1.35, 0.92])
observed = bpd.DataFrame().assign(
SampleSize=sample_sizes,
StandardDeviation=sds
)
observed.plot(kind='scatter', x='SampleSize', y='StandardDeviation', s=70, title="Standard Deviation of the Distribution of the Sample Mean vs. Sample Size", figsize=(10, 5));
It appears that as the sample size increases, the standard deviation of the distribution of the sample mean decreases quickly.
Suppose we were to take many, many samples of the same size from a population, and take the mean of each sample. Then the distribution of the sample mean will have the following characteristics:
🚨 Practical Issue: The mean and standard deviation of the distribution of the sample mean both depend on the original population, but we typically don't have access to the population!
Let's take a single sample of size 500 from delays.
np.random.seed(42)
my_sample = delays.sample(500)
my_sample.get('Delay').describe()
count 500.00
mean 13.01
std 28.00
...
50% 3.00
75% 16.00
max 209.00
Name: Delay, Length: 8, dtype: float64
Before today, to estimate the distribution of the sample mean using just this sample, we'd bootstrap:
resample_means = np.array([])
repetitions = 2000
for i in np.arange(repetitions):
resample = my_sample.sample(500, replace=True) # Bootstrapping!
resample_mean = resample.get('Delay').mean()
resample_means = np.append(resample_means, resample_mean)
resample_means
array([12.65, 11.5 , 11.34, ..., 12.59, 11.89, 12.58])
bpd.DataFrame().assign(resample_means=resample_means).plot(kind='hist', density=True, ec='w', alpha=0.65, bins=20, figsize=(10, 5));
plt.scatter([resample_means.mean()], [-0.005], marker='^', color='green', s=250)
plt.axvline(resample_means.mean(), color='green', label=f'mean={np.round(resample_means.mean(), 2)}', linewidth=4)
plt.xlim(7, 20)
plt.ylim(-0.015, 0.35)
plt.legend();
The CLT tells us what this distribution will look like, without having to bootstrap!
Now assume that all we have access to in practice is a single "original sample."
Suppose we were to bootstrap this original sample, which means we were to take many, many samples of the same size from this original sample, and take the mean of each resample. Then the distribution of the (re)sample mean will have the following characteristics:
Let's test this out!
Using just the original sample, my_sample, we estimate that the distribution of the sample mean has the following mean:
sample_mean_mean = my_sample.get('Delay').mean()
sample_mean_mean
13.008
and the following standard deviation:
sample_mean_sd = np.std(my_sample.get('Delay')) / np.sqrt(my_sample.shape[0])
sample_mean_sd
1.2511114546674091
Let's draw a normal distribution with the above mean and standard deviation, and overlay the bootstrapped distribution from earlier.
norm_x = np.linspace(7, 20)
norm_y = normal_curve(norm_x, mu=sample_mean_mean, sigma=sample_mean_sd)
bpd.DataFrame().assign(Bootstrapping=resample_means).plot(kind='hist', density=True, ec='w', alpha=0.65, bins=20, figsize=(10, 5));
plt.plot(norm_x, norm_y, color='black', linestyle='--', linewidth=4, label='CLT')
plt.title('Distribution of the Sample Mean, Using Two Methods')
plt.xlim(7, 20)
plt.legend();
Key takeaway: Given just a single sample, we can use the CLT to estimate the distribution of the sample mean, without bootstrapping.
show_clt_slides()
Now, we can make confidence intervals for population means without needing to bootstrap!
We already have a single sample, my_sample. Let's bootstrap to generate 2000 resample means.
my_sample.get('Delay').describe()
count 500.00
mean 13.01
std 28.00
...
50% 3.00
75% 16.00
max 209.00
Name: Delay, Length: 8, dtype: float64
resample_means = np.array([])
repetitions = 2000
for i in np.arange(repetitions):
resample = my_sample.sample(500, replace=True)
resample_mean = resample.get('Delay').mean()
resample_means = np.append(resample_means, resample_mean)
resample_means
array([14.37, 13.93, 11.34, ..., 16.84, 14.46, 11.4 ])
bpd.DataFrame().assign(resample_means=resample_means).plot(kind='hist', density=True, ec='w', alpha=0.65, bins=20, figsize=(10, 5));
plt.scatter([resample_means.mean()], [-0.005], marker='^', color='green', s=250)
plt.axvline(resample_means.mean(), color='green', label=f'mean={np.round(resample_means.mean(), 2)}', linewidth=4)
plt.xlim(7, 20)
plt.ylim(-0.015, 0.35)
plt.legend();
One approach to computing a confidence interval for the population mean involves taking the middle 95% of this distribution.
left_boot = np.percentile(resample_means, 2.5)
right_boot = np.percentile(resample_means, 97.5)
[left_boot, right_boot]
[10.6359, 15.61205]
bpd.DataFrame().assign(resample_means=resample_means).plot(kind='hist', y='resample_means', alpha=0.65, bins=20, density=True, ec='w', figsize=(10, 5), title='Distribution of Bootstrapped Sample Means');
plt.plot([left_boot, right_boot], [0, 0], color=gold, linewidth=12, label='95% bootstrap-based confidence interval');
plt.xlim(7, 20);
plt.legend();
But we didn't need to bootstrap to learn what the distribution of the sample mean looks like. We could instead use the CLT, which tells us that the distribution of the sample mean is normal. Further, its mean and standard deviation are approximately:
sample_mean_mean = my_sample.get('Delay').mean()
sample_mean_mean
13.008
sample_mean_sd = np.std(my_sample.get('Delay')) / np.sqrt(my_sample.shape[0])
sample_mean_sd
1.2511114546674091
So, the distribution of the sample mean is approximately:
draw_normal_curve(sample_mean_mean, sample_mean_sd)
Question: What interval on the $x$-axis captures the middle 95% of this distribution?
| Range | All Distributions (via Chebyshev's inequality) | Normal Distribution |
|---|---|---|
| mean $\pm \ 1$ SD | $\geq 0\%$ | $\approx 68\%$ |
| mean $\pm \ 2$ SDs | $\geq 75\%$ | $\approx 95\%$ |
| mean $\pm \ 3$ SDs | $\geq 88.8\%$ | $\approx 99.73\%$ |
As we saw last class, if a variable is roughly normal, then approximately 95% of its values are within 2 standard deviations of its mean.
normal_area(-2, 2)
stats.norm.cdf(2) - stats.norm.cdf(-2)
0.9544997361036416
Let's use this fact here!
left_normal = sample_mean_mean - 2 * sample_mean_sd
right_normal = sample_mean_mean + 2 * sample_mean_sd
[left_normal, right_normal]
[10.50577709066518, 15.510222909334818]
plt.figure(figsize=(10, 5))
norm_x = np.linspace(7, 20)
norm_y = normal_curve(norm_x, mu=sample_mean_mean, sigma=sample_mean_sd)
plt.plot(norm_x, norm_y, color='black', linestyle='--', linewidth=4, label='Distribution of the Sample Mean (via the CLT)')
plt.xlim(7, 20)
plt.ylim(0, 0.41)
plt.plot([left_normal, right_normal], [0, 0], color='#8f6100', linewidth=12, label='95% CLT-based confidence interval')
plt.legend();
We've constructed two confidence intervals for the population mean:
One using bootstrapping,
[left_boot, right_boot]
[10.6359, 15.61205]
and one using the CLT.
[left_normal, right_normal]
[10.50577709066518, 15.510222909334818]
In both cases, we only used information in my_sample, not the population.
The intervals created using each method are slightly different because both methods tried to approximate the true distribution of the sample mean in different ways.
A 95% confidence interval for the population mean is given by
$$ \left[\text{sample mean} - 2\cdot \frac{\text{sample SD}}{\sqrt{\text{sample size}}}, \text{sample mean} + 2\cdot \frac{\text{sample SD}}{\sqrt{\text{sample size}}} \right] $$This CI doesn't require bootstrapping, and it only requires three numbers – the sample mean, the sample SD, and the sample size!
Bootstrapping still has its uses!
| Bootstrapping | CLT | |
|---|---|---|
| Pro | Works for many sample statistics (mean, median, standard deviation). |
Only requires 3 numbers – the sample mean, sample SD, and sample size. |
| Con | Very computationally expensive (requires drawing many, many samples from the original sample). |
Only works for the sample mean (and sum). |
Note: At least for our purposes, there is no specific "minimum sample size" necessary to use either tool.
We just saw that when $z = 2$, the following is a 95% confidence interval for the population mean.
$$ \left[\text{sample mean} - z\cdot \frac{\text{sample SD}}{\sqrt{\text{sample size}}}, \text{sample mean} + z\cdot \frac{\text{sample SD}}{\sqrt{\text{sample size}}} \right] $$Question: What value of $z$ should we use to create an 80% confidence interval? 90%?
estimate_z()
HBox(children=(FloatSlider(value=2.0, description='z', max=4.0, step=0.05),))
Output()
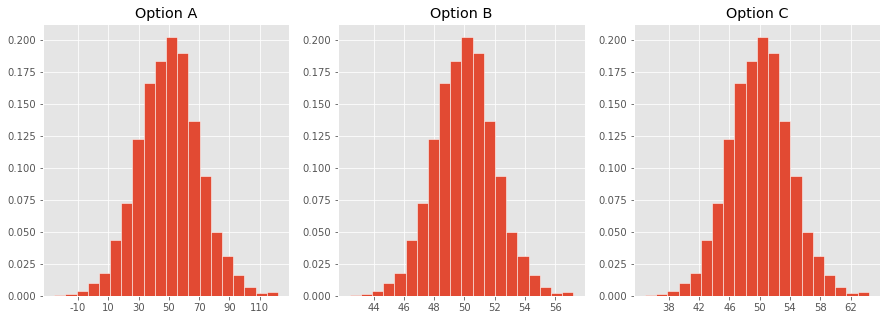
Which one of these histograms corresponds to the distribution of the sample mean for samples of size 100 drawn from a population with mean 50 and SD 20?