In [1]:
# Run this cell to set up packages for lecture.
from lec08_imports import *

Lecture 8 – Functions and Applying¶

DSC 10, Fall 2025¶

Agenda¶

  • Functions.
  • Applying functions to DataFrames.
    • Example: Student names.

*Reminder:* Use the DSC 10 Reference Sheet.

Functions¶

Defining functions¶

  • We've learned how to do quite a bit in Python:
    • Manipulate arrays, Series, and DataFrames.
    • Perform operations on strings.
    • Create visualizations.
  • But so far, we've been restricted to using existing functions (e.g. max, np.sqrt, len) and methods (e.g. .groupby, .assign, .plot).

Motivation¶

  • In Homework 1, you made an array containing all the multiples of 10, in ascending order, that appear on the multiplication table below.

In [2]:
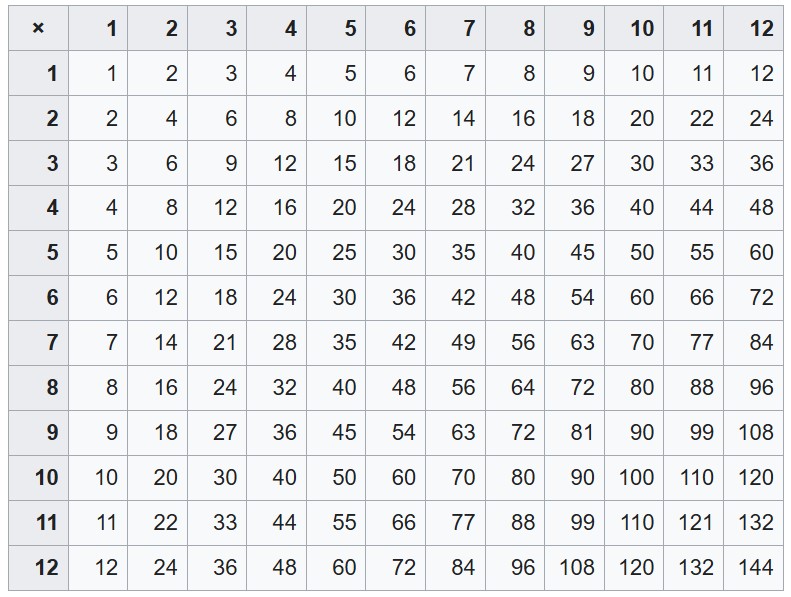
multiples_of_10 = np.arange(10, 130, 10)
multiples_of_10
Out[2]:
array([ 10,  20,  30,  40,  50,  60,  70,  80,  90, 100, 110, 120])
  • Question: How would you make an array containing all the multiples of 8, in increasing order, that appear on the multiplication table?
In [3]:
multiples_of_8 = np.arange(8, 13*8, 8)
multiples_of_8
Out[3]:
array([ 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96])

More generally¶

What if we want to find the multiples of some other number, k? We can copy-paste and change some numbers, but that is prone to error.

In [4]:
multiples_of_5 = ...
multiples_of_5
Out[4]:
Ellipsis

It turns out that we can define our own "multiples" function just once, and re-use it many times for different values of k. 🔁

In [5]:
def multiples(k):
    '''This function returns the 
    first twelve multiples of k.'''
    return np.arange(k, 13*k, k)
In [6]:
multiples(8)
Out[6]:
array([ 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96])
In [7]:
multiples(5)
Out[7]:
array([ 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60])

Note that we only had to specify how to calculate multiples a single time!

Functions¶

Functions are a way to divide our code into small subparts to prevent us from writing repetitive code. Each time we define our own function in Python, we will use the following pattern.

In [8]:
show_def()

Functions are "recipes"¶

  • Functions take in inputs, known as arguments, do something, and produce some outputs.
  • The beauty of functions is that you don't need to know how they are implemented in order to use them!
    • For instance, you've been using the function bpd.read_csv without knowing how it works.
    • This is the premise of the idea of abstraction in computer science – you'll hear a lot about this if you take DSC 20.
In [9]:
multiples(7)
Out[9]:
array([ 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84])
In [10]:
multiples(-2)
Out[10]:
array([ -2,  -4,  -6,  -8, -10, -12, -14, -16, -18, -20, -22, -24])

Parameters and arguments¶

triple has one parameter, x.

In [11]:
def triple(x):
    return x * 3

When we call triple with the argument 5, within the body of triple, x means 5.

In [12]:
triple(5)
Out[12]:
15

We can call triple with other arguments, even strings!

In [13]:
triple(7 + 8)
Out[13]:
45
In [14]:
triple('triton')
Out[14]:
'tritontritontriton'

Scope 🩺¶

The names you choose for a function’s parameters are only known to that function (known as local scope). The rest of your notebook is unaffected by parameter names.

In [15]:
def triple(x):
    return x * 3
In [16]:
triple(7)
Out[16]:
21

Since we haven't defined an x outside of the body of triple, our notebook doesn't know what x means.

In [17]:
x

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
/tmp/ipykernel_181/32546335.py in <module>
----> 1 x

NameError: name 'x' is not defined

We can define an x outside of the body of triple, but that doesn't change how triple works.

In [18]:
x = 15
In [19]:
# When triple(12) is called, you can pretend
# there's an invisible line inside the body of x
# that says x = 12.
# The x = 15 above is ignored.
triple(12)
Out[19]:
36

Functions can take 0 or more arguments¶

Functions can take any number of arguments.

greeting takes no arguments.

In [20]:
def greeting():
    return 'Hi! 👋'
In [21]:
greeting()
Out[21]:
'Hi! 👋'

custom_multiples takes two arguments!

In [22]:
def custom_multiples(k, how_many):
    '''This function returns the 
    first how_many multiples of k.'''
    return np.arange(k, (how_many + 1)*k, k)
In [23]:
custom_multiples(10, 7)
Out[23]:
array([10, 20, 30, 40, 50, 60, 70])
In [24]:
custom_multiples(2, 100)
Out[24]:
array([  2,   4,   6, ..., 196, 198, 200])

Functions don't run until you call them!¶

The body of a function is not run until you use (call) the function.

Here, we can define where_is_the_error without seeing an error message.

In [25]:
def where_is_the_error(something):
    '''A function to illustrate that errors don't occur 
    until functions are executed (called).'''
    return (1 / 0) + something

It is only when we call where_is_the_error that Python gives us an error message.

In [26]:
where_is_the_error(5)

---------------------------------------------------------------------------
ZeroDivisionError                         Traceback (most recent call last)
/tmp/ipykernel_181/3423408763.py in <module>
----> 1 where_is_the_error(5)

/tmp/ipykernel_181/3410008411.py in where_is_the_error(something)
      2     '''A function to illustrate that errors don't occur 
      3     until functions are executed (called).'''
----> 4     return (1 / 0) + something

ZeroDivisionError: division by zero

Example: first_name¶

Let's create a function called first_name that takes in someone's full name and returns their first name. Example behavior is shown below.

>>> first_name('Pradeep Khosla')
'Pradeep'

Hint: Use the string method .split.

General strategy for writing functions:

  1. First, try and get the behavior to work on a single example.
  2. Then, encapsulate that behavior inside a function.
In [ ]:
In [27]:
'Pradeep Khosla'.split(' ')[0]
Out[27]:
'Pradeep'
In [28]:
def first_name(full_name):
    '''Returns the first name given a full name.'''
    return full_name.split(' ')[0]
In [29]:
first_name('Pradeep Khosla')
Out[29]:
'Pradeep'
In [30]:
# What if there are three names?
first_name('Chancellor Pradeep Khosla')
Out[30]:
'Chancellor'

Returning¶

  • The return keyword specifies what the output of your function should be, i.e. what a call to your function will evaluate to.
  • Some functions don't have any output and don't use return.
    • If you want to be able to save the output of your function to a variable, you must use return!
  • Be careful: print and return work differently!
In [31]:
def pythagorean(a, b):
    '''Computes the hypotenuse length of a right triangle with legs a and b.'''
    c = (a ** 2 + b ** 2) ** 0.5
    print(c)
In [32]:
x = pythagorean(3, 4)

5.0
In [33]:
# No output – why?
x
In [34]:
# Errors – why?
x + 10

---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
/tmp/ipykernel_181/3707561498.py in <module>
      1 # Errors – why?
----> 2 x + 10

TypeError: unsupported operand type(s) for +: 'NoneType' and 'int'
In [35]:
def better_pythagorean(a, b):
    '''Computes the hypotenuse length of a right triangle with legs a and b, 
       and actually returns the result.
    '''
    c = (a ** 2 + b ** 2) ** 0.5
    return c
In [36]:
x = better_pythagorean(3, 4)
x
Out[36]:
5.0
In [37]:
x + 10
Out[37]:
15.0

Returning¶

Once a function executes a return statement, it stops running.

In [38]:
def motivational(quote):
    return 0
    print("Here's a motivational quote:", quote)
In [39]:
motivational('Fall seven times and stand up eight.')
Out[39]:
0

Applying functions to DataFrames¶

DSC 10 student data¶

The DataFrame roster contains the names and lecture sections of all students enrolled in DSC 10 this quarter. The first names are real, while the last names have been anonymized for privacy.

In [40]:
roster = bpd.read_csv('data/roster-anon.csv')
roster
Out[40]:
name section
0 Camilla Ozqcfu B
1 Yifan Ignjpe A
2 Ali Jjsojh A
... ... ...
491 Qiankang Tzjsbb D
492 Kim Wxnmuh C
493 Jazmine Sxcvft C

494 rows × 2 columns

Example: Common first names¶

What is the most common first name among DSC 10 students? (Any guesses?)

In [41]:
roster
Out[41]:
name section
0 Camilla Ozqcfu B
1 Yifan Ignjpe A
2 Ali Jjsojh A
... ... ...
491 Qiankang Tzjsbb D
492 Kim Wxnmuh C
493 Jazmine Sxcvft C

494 rows × 2 columns

  • Problem: We can't answer that right now, since we don't have a column with first names. If we did, we could group by it.
  • Solution: Use our function that extracts first names on every element of the 'name' column.

Using our first_name function¶

Somehow, we need to call first_name on every student's 'name'.

In [42]:
roster
Out[42]:
name section
0 Camilla Ozqcfu B
1 Yifan Ignjpe A
2 Ali Jjsojh A
... ... ...
491 Qiankang Tzjsbb D
492 Kim Wxnmuh C
493 Jazmine Sxcvft C

494 rows × 2 columns

In [43]:
roster.get('name').iloc[0]
Out[43]:
'Camilla Ozqcfu'
In [44]:
first_name(roster.get('name').iloc[0])
Out[44]:
'Camilla'
In [45]:
first_name(roster.get('name').iloc[1])
Out[45]:
'Yifan'

Ideally, there's a better solution than doing this hundreds of times...

.apply¶

  • To apply the function func_name to every element of column 'col' in DataFrame df, use
df.get('col').apply(func_name)
  • The .apply method is a Series method.
    • Important: We use .apply on Series, not DataFrames.
    • The output of .apply is also a Series.
  • Pass just the name of the function – don't call it!
    • Good ✅: .apply(first_name).
    • Bad ❌: .apply(first_name()).
In [46]:
roster.get('name')
Out[46]:
0       Camilla Ozqcfu
1         Yifan Ignjpe
2           Ali Jjsojh
            ...       
491    Qiankang Tzjsbb
492         Kim Wxnmuh
493     Jazmine Sxcvft
Name: name, Length: 494, dtype: object
In [47]:
roster.get('name').apply(first_name)
Out[47]:
0       Camilla
1         Yifan
2           Ali
         ...   
491    Qiankang
492         Kim
493     Jazmine
Name: name, Length: 494, dtype: object

Example: Common first names¶

In [48]:
roster = roster.assign(
    first=roster.get('name').apply(first_name)
)
roster
Out[48]:
name section first
0 Camilla Ozqcfu B Camilla
1 Yifan Ignjpe A Yifan
2 Ali Jjsojh A Ali
... ... ... ...
491 Qiankang Tzjsbb D Qiankang
492 Kim Wxnmuh C Kim
493 Jazmine Sxcvft C Jazmine

494 rows × 3 columns

Now that we have a column containing first names, we can find the distribution of first names.

In [49]:
name_counts = (
    roster
    .groupby('first')
    .count()
    .sort_values('name', ascending=False)
    .get(['name'])
)
name_counts
Out[49]:
name
first
Andrew 7
Noah 5
Joseph 5
... ...
Heaven 1
Harsh 1
Ziyong 1

427 rows × 1 columns

Activity¶

Below:

  • Create a bar chart showing the number of students with each first name, but only include first names shared by at least two students.
  • Determine the proportion of students in DSC 10 who have a first name that is shared by at least two students.

Hint: Start by defining a DataFrame with only the names in name_counts that appeared at least twice. You can use this DataFrame to answer both questions.


✅ Click here to see the solutions after you've tried it yourself. 

shared_names = name_counts[name_counts.get('name') >= 2]

# Bar chart.
shared_names.sort_values('name').plot(kind='barh', y='name', figsize=(5, 8));

# Proportion = # students with a shared name / total # of students.
shared_names.get('name').sum() / roster.shape[0]
In [50]:
...
Out[50]:
Ellipsis
In [51]:
...
Out[51]:
Ellipsis

.apply works with built-in functions, too!¶

In [52]:
name_counts.get('name')
Out[52]:
first
Andrew    7
Noah      5
Joseph    5
         ..
Heaven    1
Harsh     1
Ziyong    1
Name: name, Length: 427, dtype: int64
In [53]:
# Not necessarily meaningful, but doable.
name_counts.get('name').apply(np.log)
Out[53]:
first
Andrew    1.95
Noah      1.61
Joseph    1.61
          ... 
Heaven    0.00
Harsh     0.00
Ziyong    0.00
Name: name, Length: 427, dtype: float64

Aside: Resetting the index¶

In name_counts, first names are stored in the index, which is not a Series. This means we can't use .apply on it.

In [54]:
name_counts.index
Out[54]:
Index(['Andrew', 'Noah', 'Joseph', 'Ethan', 'Michael', 'Christopher', 'Daniel',
       'Justin', 'Abhinav', 'Jaden',
       ...
       'Ingkawat', 'I-Shan', 'Humza', 'Huilin', 'Honoka', 'Hirkani', 'Hilary',
       'Heaven', 'Harsh', 'Ziyong'],
      dtype='object', name='first', length=427)
In [55]:
name_counts.index.apply(max)

---------------------------------------------------------------------------
AttributeError                            Traceback (most recent call last)
/tmp/ipykernel_181/1905262767.py in <module>
----> 1 name_counts.index.apply(max)

AttributeError: 'Index' object has no attribute 'apply'

To help, we can use .reset_index() to turn the index of a DataFrame into a column, and to reset the index back to the default of 0, 1, 2, 3, and so on.

In [56]:
# What is the max of an individual string?
name_counts.reset_index().get('first').apply(max)
Out[56]:
0      w
1      o
2      s
      ..
424    v
425    s
426    y
Name: first, Length: 427, dtype: object

Example: Shared first names and sections¶

  • Suppose you're one of the students who has a first name that is shared with at least one other student.
  • Let's try and determine whether someone in your lecture section shares the same first name as you.
    • For example, maybe 'Jayden Lcaert' wants to see if there's another 'Jayden' in their section.

Strategy:

  1. Which section is 'Jayden Lcaert' in?
  2. How many people in that section have a first name of 'Jayden'?
In [57]:
roster
Out[57]:
name section first
0 Camilla Ozqcfu B Camilla
1 Yifan Ignjpe A Yifan
2 Ali Jjsojh A Ali
... ... ... ...
491 Qiankang Tzjsbb D Qiankang
492 Kim Wxnmuh C Kim
493 Jazmine Sxcvft C Jazmine

494 rows × 3 columns

In [58]:
which_section = roster[roster.get('name') == 'Jayden Lcaert'].get('section').iloc[0]
which_section
Out[58]:
'B'
In [59]:
first_cond = roster.get('first') == 'Jayden' # A Boolean Series!
section_cond = roster.get('section') == which_section # A Boolean Series!
how_many = roster[first_cond & section_cond].shape[0]
how_many
Out[59]:
2

Another function: shared_first_and_section¶

Let's create a function named shared_first_and_section. It will take in the full name of a student and return the number of students in their section with the same first name and section (including them).

Note: This is the first function we're writing that involves using a DataFrame within the function – this is fine!

In [60]:
def shared_first_and_section(name):
    # First, find the row corresponding to that full name in roster.
    # We're assuming that full names are unique.
    row = roster[roster.get('name') == name]
    
    # Then, get that student's first name and section.
    first = row.get('first').iloc[0]
    section = row.get('section').iloc[0]
    
    # Now, find all the students with the same first name and section.
    shared_info = roster[(roster.get('first') == first) & (roster.get('section') == section)]
    
    # Return the number of such students.
    return shared_info.shape[0]
In [61]:
shared_first_and_section('Jayden Lcaert')
Out[61]:
2

Now, let's add a column to roster that contains the values returned by shared_first_and_section.

In [62]:
roster = roster.assign(shared=roster.get('name').apply(shared_first_and_section))
roster
Out[62]:
name section first shared
0 Camilla Ozqcfu B Camilla 1
1 Yifan Ignjpe A Yifan 1
2 Ali Jjsojh A Ali 2
... ... ... ... ...
491 Qiankang Tzjsbb D Qiankang 1
492 Kim Wxnmuh C Kim 1
493 Jazmine Sxcvft C Jazmine 1

494 rows × 4 columns

Let's find all of the students who are in a section with someone that has the same first name as them.

In [63]:
roster[(roster.get('shared') >= 2)].sort_values('shared', ascending=False)
Out[63]:
name section first shared
486 Joseph Jpoelz C Joseph 4
411 Joseph Vdhfyo C Joseph 4
329 Joseph Jaqwhh C Joseph 4
... ... ... ... ...
226 William Mjsrep D William 2
154 Jayden Lcaert B Jayden 2
2 Ali Jjsojh A Ali 2

46 rows × 4 columns

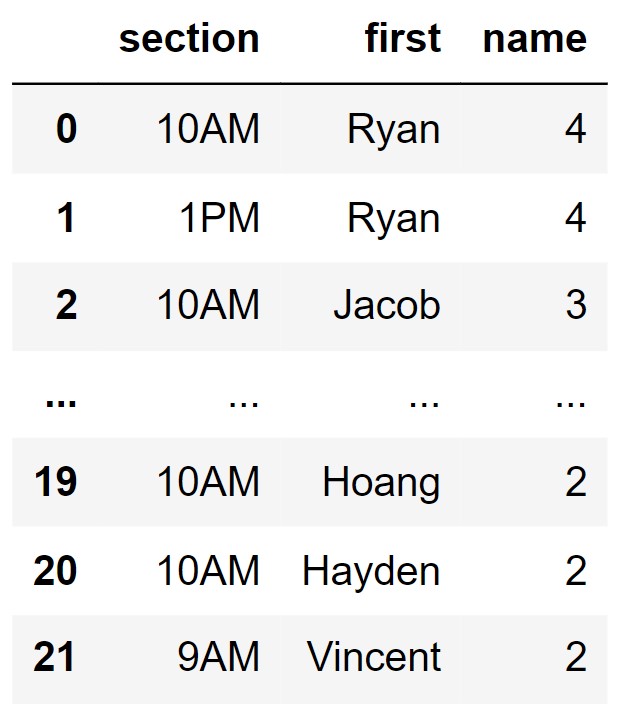
Sneak peek¶

While the DataFrame above contains the information we were looking for, it is not organized very conveniently and it is somewhat redundant.

Wouldn't it be great if we could create a DataFrame like the one below? We'll see how next time!

Activity¶

Find the longest first name in the class that is shared by at least two students in the same section.

Hint: You'll have to use both .assign and .apply.


✅ Click here to see the answer after you've tried it yourself. 

with_len = roster.assign(name_len=roster.get('first').apply(len))
with_len[with_len.get('shared') >= 2].sort_values('name_len', ascending=False).get('first').iloc[0]
In [64]:
...
Out[64]:
Ellipsis

Summary, next time¶

Summary¶

  • Functions are a way to divide our code into small subparts to prevent us from writing repetitive code.
  • The .apply method allows us to call a function on every single element of a Series, which usually comes from .getting a column of a DataFrame.

Next time¶

More advanced DataFrame manipulations!