In [1]:
# Run this cell to set up packages for lecture.
from lec05_imports_2 import *

Lecture 5: Part 2: Functions¶

DSC 10, Summer 2025¶

Agenda¶

  • Functions.

Reminder: Use the DSC 10 Reference Sheet.

Functions¶

Defining functions¶

  • We've learned how to do quite a bit in Python:
    • Manipulate arrays, Series, and DataFrames.
    • Perform operations on strings.
    • Create visualizations.
  • But so far, we've been restricted to using existing functions (e.g. max, np.sqrt, len) and methods (e.g. .groupby, .assign, .plot).

Motivation¶

  • In Homework 1, you made an array containing all the multiples of 10, in ascending order, that appear on the multiplication table below.

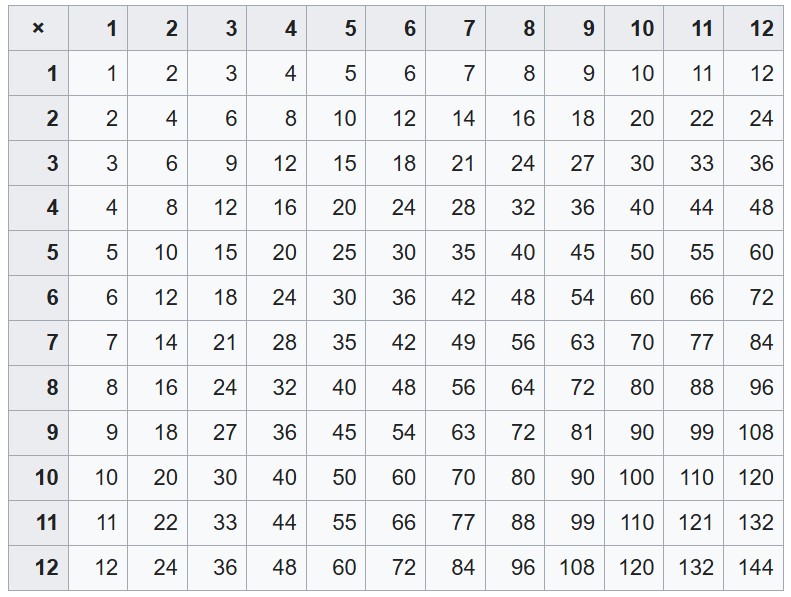
    No description has been provided for this image
In [2]:
multiples_of_10 = np.arange(10, 130, 10)
multiples_of_10
Out[2]:
array([ 10,  20,  30,  40,  50,  60,  70,  80,  90, 100, 110, 120])
  • Question: How would you make an array containing all the multiples of 8, in increasing order, that appear on the multiplication table?
In [3]:
multiples_of_8 = np.arange(8, 13*8, 8)
multiples_of_8
Out[3]:
array([ 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96])

More generally¶

What if we want to find the multiples of some other number, k? We can copy-paste and change some numbers, but that is prone to error.

In [4]:
multiples_of_5 = ...
multiples_of_5
Out[4]:
Ellipsis

It turns out that we can define our own "multiples" function just once, and re-use it many times for different values of k. 🔁

In [5]:
def multiples(k):
    '''This function returns the 
    first twelve multiples of k.'''
    return np.arange(k, 13*k, k)
In [6]:
multiples(8)
Out[6]:
array([ 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96])
In [7]:
multiples(5)
Out[7]:
array([ 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60])

Note that we only had to specify how to calculate multiples a single time!

Functions¶

Functions are a way to divide our code into small subparts to prevent us from writing repetitive code. Each time we define our own function in Python, we will use the following pattern.

In [8]:
show_def()

Functions are "recipes"¶

  • Functions take in inputs, known as arguments, do something, and produce some outputs.
  • The beauty of functions is that you don't need to know how they are implemented in order to use them!
    • For instance, you've been using the function bpd.read_csv without knowing how it works.
    • This is the premise of the idea of abstraction in computer science – you'll hear a lot about this if you take DSC 20.
In [9]:
multiples(7)
Out[9]:
array([ 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84])
In [10]:
multiples(-2)
Out[10]:
array([ -2,  -4,  -6,  -8, -10, -12, -14, -16, -18, -20, -22, -24])

Parameters and arguments¶

triple has one parameter, x.

In [11]:
def triple(x):
    return x * 3

When we call triple with the argument 5, within the body of triple, x means 5.

In [12]:
triple(5)
Out[12]:
15

We can change the argument we call triple with – we can even call it with strings!

In [13]:
triple(7 + 8)
Out[13]:
45
In [14]:
triple('triton')
Out[14]:
'tritontritontriton'

Scope 🩺¶

The names you choose for a function’s parameters are only known to that function (known as local scope). The rest of your notebook is unaffected by parameter names.

In [15]:
def triple(x):
    return x * 3
In [16]:
triple(7)
Out[16]:
21

Since we haven't defined an x outside of the body of triple, our notebook doesn't know what x means.

In [17]:
x

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
/var/folders/2k/9mnd960x2j1d9b35wyjwwx200000gp/T/ipykernel_72237/32546335.py in <cell line: 0>()
----> 1 x

NameError: name 'x' is not defined

We can define an x outside of the body of triple, but that doesn't change how triple works.

In [18]:
x = 15
In [19]:
# When triple(12) is called, you can pretend
# there's an invisible line inside the body of x
# that says x = 12.
# The x = 15 above is ignored.
triple(12)
Out[19]:
36

Functions can take 0 or more arguments¶

Functions can take any number of arguments.

greeting takes no arguments.

In [20]:
def greeting():
    return 'Hi! 👋'
In [21]:
greeting()
Out[21]:
'Hi! 👋'

custom_multiples takes two arguments!

In [22]:
def custom_multiples(k, how_many):
    '''This function returns the 
    first how_many multiples of k.'''
    return np.arange(k, (how_many + 1)*k, k)
In [23]:
custom_multiples(10, 7)
Out[23]:
array([10, 20, 30, 40, 50, 60, 70])
In [24]:
custom_multiples(2, 100)
Out[24]:
array([  2,   4,   6, ..., 196, 198, 200])

Functions don't run until you call them!¶

The body of a function is not run until you use (call) the function.

Here, we can define where_is_the_error without seeing an error message.

In [25]:
def where_is_the_error(something):
    '''A function to illustrate that errors don't occur 
    until functions are executed (called).'''
    return (1 / 0) + something

It is only when we call where_is_the_error that Python gives us an error message.

In [26]:
where_is_the_error(5)

---------------------------------------------------------------------------
ZeroDivisionError                         Traceback (most recent call last)
/var/folders/2k/9mnd960x2j1d9b35wyjwwx200000gp/T/ipykernel_72237/3423408763.py in <cell line: 0>()
----> 1 where_is_the_error(5)

/var/folders/2k/9mnd960x2j1d9b35wyjwwx200000gp/T/ipykernel_72237/3410008411.py in where_is_the_error(something)
      2     '''A function to illustrate that errors don't occur 
      3     until functions are executed (called).'''
----> 4     return (1 / 0) + something

ZeroDivisionError: division by zero

Example: first_name¶

Let's create a function called first_name that takes in someone's full name and returns their first name. Example behavior is shown below.

>>> first_name('Pradeep Khosla')
'Pradeep'

Hint: Use the string method .split.

General strategy for writing functions:

  1. First, try and get the behavior to work on a single example.
  2. Then, encapsulate that behavior inside a function.
In [27]:
'Pradeep Khosla'.split(' ')[0]
Out[27]:
'Pradeep'
In [28]:
def first_name(full_name):
    '''Returns the first name given a full name.'''
    return full_name.split(' ')[0]
In [29]:
first_name('Pradeep Khosla')
Out[29]:
'Pradeep'
In [30]:
# What if there are three names?
first_name('Chancellor Pradeep Khosla')
Out[30]:
'Chancellor'

Returning¶

  • The return keyword specifies what the output of your function should be, i.e. what a call to your function will evaluate to.
  • Most functions we write will use return, but using return is not strictly required.
    • If you want to be able to save the output of your function to a variable, you must use return!
  • Be careful: print and return work differently!
In [31]:
def pythagorean(a, b):
    '''Computes the hypotenuse length of a right triangle with legs a and b.'''
    c = (a ** 2 + b ** 2) ** 0.5
    print(c)
In [32]:
x = pythagorean(3, 4)

5.0
In [33]:
# No output – why?
x
In [34]:
# Errors – why?
x + 10

---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
/var/folders/2k/9mnd960x2j1d9b35wyjwwx200000gp/T/ipykernel_72237/3305400239.py in <cell line: 0>()
      1 # Errors – why?
----> 2 x + 10

TypeError: unsupported operand type(s) for +: 'NoneType' and 'int'
In [35]:
def better_pythagorean(a, b):
    '''Computes the hypotenuse length of a right triangle with legs a and b, 
       and actually returns the result.
    '''
    c = (a ** 2 + b ** 2) ** 0.5
    return c
In [36]:
x = better_pythagorean(3, 4)
x
Out[36]:
5.0
In [37]:
x + 10
Out[37]:
15.0

Returning¶

Once a function executes a return statement, it stops running.

In [38]:
def motivational(quote):
    return 0
    print("Here's a motivational quote:", quote)
In [39]:
motivational('Fall seven times and stand up eight.')
Out[39]:
0