In [1]:
# Run this cell to set up packages for lecture.
from lec17_imports import *

Lecture 17 – Standardization and the Normal Distribution¶

DSC 10, Fall 2024¶

Announcements¶

  • Lab 4 is due Thursday and Homework 4 is due Sunday.
  • Monday is Veteran's Day, which is a university holiday. There will be no lecture, no discussion, and no office hours on Monday.

Agenda¶

  • Chebyshev's inequality.
  • Standardization.
  • The normal distribution.

Chebyshev's inequality¶

Recap: variance and standard deviation¶

$$\begin{align*}\text{variance} &= \text{average squared deviation from the mean}\\ &= \frac{(\text{value}_1 - \text{mean})^2 + ... + (\text{value}_n - \text{mean})^2}{n}\\ \text{standard deviation} &= \sqrt{\text{variance}} \end{align*}$$

where $n$ is the number of observations.

Standard deviation¶

  • The standard deviation (SD) measures something about how far the data values are from their average.
    • It is not directly interpretable because of the squaring and square rooting.
    • But generally, larger SD = more spread out.
  • The standard deviation has the same units as the original data.
  • numpy has a function, np.std, that calculates the standard deviation for us.
In [2]:
np.std([2, 3, 3, 9])
Out[2]:
2.7726341266023544

What can we do with the standard deviation?¶

It turns out, in any numerical distribution, the bulk of the data are in the range “mean ± a few SDs”.

Let's make this more precise.

Chebyshev’s inequality¶

Fact: In any numerical distribution, the proportion of values in the range “mean ± $z$ SDs” is at least

$$1 - \frac{1}{z^2} $$

Range Proportion
mean ± 2 SDs at least $1 - \frac{1}{4}$ (75%)
mean ± 3 SDs at least $1 - \frac{1}{9}$ (88.88..%)
mean ± 4 SDs at least $1 - \frac{1}{16}$ (93.75%)
mean ± 5 SDs at least $1 - \frac{1}{25}$ (96%)

Flight delays, revisited ✈️¶

In [3]:
delays = bpd.read_csv('data/united_summer2015.csv')
delays.plot(kind='hist', y='Delay', bins=np.arange(-20.5, 210, 5), density=True, ec='w', figsize=(10, 5), title='Flight Delays')
plt.xlabel('Delay (minutes)');
No description has been provided for this image
In [4]:
delay_mean = delays.get('Delay').mean()
delay_mean
Out[4]:
16.658155515370705
In [5]:
delay_std = np.std(delays.get('Delay')) # There is no .std() method in babypandas!
delay_std
Out[5]:
39.480199851609314

Mean and standard deviation¶

Chebyshev's inequality tells us that

  • At least 75% of delays are in the following interval:
In [6]:
delay_mean - 2 * delay_std, delay_mean + 2 * delay_std
Out[6]:
(-62.30224418784792, 95.61855521858934)
  • At least 88.88% of delays are in the following interval:
In [7]:
delay_mean - 3 * delay_std, delay_mean + 3 * delay_std
Out[7]:
(-101.78244403945723, 135.09875507019865)

Let's visualize these intervals!

In [8]:
delays.plot(kind='hist', y='Delay', bins=np.arange(-20.5, 210, 5), density=True, alpha=0.65, ec='w', figsize=(10, 5), title='Flight Delays')
plt.axvline(delay_mean - 2 * delay_std, color='maroon', label='± 2 SD')
plt.axvline(delay_mean + 2 * delay_std, color='maroon')

plt.axvline(delay_mean + 3 * delay_std, color='blue',  label='± 3 SD')
plt.axvline(delay_mean - 3 * delay_std, color='blue')

plt.axvline(delay_mean, color='green', label='Mean')
plt.scatter([delay_mean], [-0.0017], color='green', marker='^', s=250)
plt.ylim(-0.0038, 0.06)
plt.legend();
No description has been provided for this image

Chebyshev's inequality provides lower bounds!¶

Remember, Chebyshev's inequality states that at least $1 - \frac{1}{z^2}$ of values are within $z$ SDs from the mean, for any numerical distribution.

For instance, it tells us that at least 75% of delays are in the following interval:

In [9]:
delay_mean - 2 * delay_std, delay_mean + 2 * delay_std
Out[9]:
(-62.30224418784792, 95.61855521858934)

However, in this case, a much larger fraction of delays are in that interval.

In [10]:
within_2_sds = delays[(delays.get('Delay') >= delay_mean - 2 * delay_std) & 
                      (delays.get('Delay') <= delay_mean + 2 * delay_std)]

within_2_sds.shape[0] / delays.shape[0]
Out[10]:
0.9560940325497288

If we know more about the shape of the distribution, we can provide better guarantees for the proportion of values within $z$ SDs of the mean.

Activity¶

For a particular set of data points, Chebyshev's inequality states that at least $\frac{8}{9}$ of the data points are between $-20$ and $40$. What is the standard deviation of the data?

✅ Click here to see the answer after you've tried it yourself.
  • Chebyshev's inequality states that at least $1 - \frac{1}{z^2}$ of values are within $z$ standard deviations of the mean.
  • When $z = 3$, $1 - \frac{1}{z^2} = \frac{8}{9}$.
  • So, $-20$ is $3$ standard deviations below the mean, and $40$ is $3$ standard deviations above the mean.
  • $10$ is in the middle of $-20$ and $40$, so the mean is $10$.
  • $3$ standard deviations are between $10$ and $40$, so $1$ standard deviation is $\frac{30}{3} = 10$.

Standardization¶

Heights and weights 📏¶

We'll work with a data set containing the heights and weights of 5000 adult males.

In [11]:
height_and_weight = bpd.read_csv('data/height_and_weight.csv')
height_and_weight
Out[11]:
Height Weight
0 73.85 241.89
1 68.78 162.31
2 74.11 212.74
... ... ...
4997 67.01 199.20
4998 71.56 185.91
4999 70.35 198.90

5000 rows × 2 columns

Distributions of height and weight¶

Let's look at the distributions of both numerical variables.

In [12]:
height_and_weight.plot(kind='hist', y='Height', density=True, ec='w', bins=30, alpha=0.8, figsize=(10, 5));
No description has been provided for this image
In [13]:
height_and_weight.plot(kind='hist', y='Weight', density=True, ec='w', bins=30, alpha=0.8, color='C1', figsize=(10, 5));
No description has been provided for this image
In [14]:
height_and_weight.plot(kind='hist', density=True, ec='w', bins=60, alpha=0.8, figsize=(10, 5));
No description has been provided for this image

Observation: The two distributions look like shifted and stretched versions of the same basic shape, called a bell curve 🔔. Distributions shaped like this are called normal distributions.

Many normal distributions¶

  • There are many normal distributions, with different means and different standard deviations.
  • All normal distributions are shaped like bell curves, but they vary in center and spread.
  • The mean and standard deviation uniquely define a normal distribution. There is only one normal distribution with a given mean and SD.
In [15]:
show_many_normal_distributions()
No description has been provided for this image
  • Note that the area underneath each curve is 1. Therefore, the taller curves are narrower, and the shorter curves are wider.
  • Any normal distribution can be shifted and scaled to look like any other normal distribution. Let's see how with height and weight!

Standard units¶

Suppose $x$ is a numerical variable, and $x_i$ is one value of that variable. Then, $$x_{i \: \text{(su)}} = \frac{x_i - \text{mean of $x$}}{\text{SD of $x$}}$$

represents $x_i$ in standard units – the number of standard deviations $x_i$ is above the mean.

Example: Suppose someone weighs 225 pounds. What is their weight in standard units?

In [16]:
weights = height_and_weight.get('Weight')
(225 - weights.mean()) / np.std(weights)
Out[16]:
1.9201699181580782
  • Interpretation: 225 is 1.92 standard deviations above the mean weight.
  • 225 becomes 1.92 in standard units.

Standardization¶

The process of converting all values of a variable (i.e. a column) to standard units is known as standardization, and the resulting values are considered to be standardized.

In [17]:
def standard_units(col):
    return (col - col.mean()) / np.std(col)
In [18]:
standardized_height = standard_units(height_and_weight.get('Height'))
standardized_height
Out[18]:
0       1.68
1      -0.09
2       1.78
        ... 
4997   -0.70
4998    0.88
4999    0.46
Name: Height, Length: 5000, dtype: float64
In [19]:
standardized_weight = standard_units(height_and_weight.get('Weight'))
standardized_weight
Out[19]:
0       2.77
1      -1.25
2       1.30
        ... 
4997    0.62
4998   -0.06
4999    0.60
Name: Weight, Length: 5000, dtype: float64

The effect of standardization¶

Standardized variables have:

  • A mean of 0.
  • An SD of 1.

We often standardize variables to bring them to the same scale.

In [20]:
# e-15 means 10^(-15), which is a very small number, effectively zero.
standardized_height.describe()
Out[20]:
count    5.00e+03
mean     1.49e-15
std      1.00e+00
           ...   
50%      4.76e-04
75%      6.85e-01
max      3.48e+00
Name: Height, Length: 8, dtype: float64
In [21]:
standardized_weight.describe()
Out[21]:
count    5.00e+03
mean     5.98e-16
std      1.00e+00
           ...   
50%      6.53e-04
75%      6.74e-01
max      4.19e+00
Name: Weight, Length: 8, dtype: float64

Let's look at how the process of standardization works visually.

In [22]:
HTML('data/height_anim.html')
Out[22]:
Your browser does not support the video tag.
In [23]:
HTML('data/weight_anim.html')
Out[23]:
Your browser does not support the video tag.

Standardized histograms¶

Now that we've standardized the distributions of height and weight, let's see how they look on the same set of axes.

In [24]:
standardized_height_and_weight = bpd.DataFrame().assign(
    Height=standardized_height,
    Weight=standardized_weight
)
standardized_height_and_weight.plot(kind='hist', density=True, ec='w',bins=30, alpha=0.8, figsize=(10, 5));
No description has been provided for this image

These both look very similar!

The standard normal distribution¶

The standard normal distribution¶

  • The distributions we've seen look essentially the same once standardized.
  • This distribution is called the standard normal distribution. It is defined by its mean of 0 and its standard deviation of 1. The shape of such a distribution is called the standard normal curve.

$$ \phi(z) = \frac{1}{\sqrt{2 \pi}} e^{-\frac{1}{2}z^2} $$

  • You don't need to know the formula – just the shape!
    • We'll just use the formula today to make plots.

The standard normal curve¶

In [25]:
def normal_curve(z):
    return 1 / np.sqrt(2 * np.pi) * np.exp((-z**2)/2)

x = np.linspace(-4, 4, 1000)
y = normal_curve(x)

plt.figure(figsize=(10, 5))
plt.plot(x, y, color='black');
plt.xlabel('$z$');
plt.title(r'$\phi(z) = \frac{1}{\sqrt{2 \pi}} e^{-\frac{1}{2}z^2}$');
No description has been provided for this image

Heights/weights are roughly normal¶

If a distribution follows this shape, we say it is roughly normal.

In [26]:
standardized_height_and_weight.plot(kind='hist', density=True, ec='w', bins=120, alpha=0.8, figsize=(10, 5));
plt.plot(x, y, color='black', linestyle='--', label='Normal', linewidth=5)
plt.legend(loc='upper right');
No description has been provided for this image

The standard normal distribution¶

  • Think of the normal distribution as a "continuous histogram".
  • Its mean and median are both 0 – it is symmetric.
  • It has inflection points at $\pm 1$.
    • More on this later.
  • Like a histogram:
    • The area between $a$ and $b$ is the proportion of values between $a$ and $b$.
    • The total area underneath the normal curve is is 1.
In [27]:
sliders()

HBox(children=(FloatSlider(value=0.0, description='a', max=3.0, min=-4.0, step=0.25), FloatSlider(value=1.0, d…
Output()

Cumulative density functions¶

  • The cumulative density function (CDF) of a distribution is a function that takes in a value $z$ and returns the proportion of values in the distribution that are less than or equal to $z$, i.e. the area under the curve to the left of $z$.
  • To find areas under curves, we typically use integration (calculus). However, the standard normal curve has no closed-form integral.
  • Often, people refer to tables that contain approximations of the CDF of the standard normal distribution.
  • We'll use an approximation built into the scipy module in Python. The function scipy.stats.norm.cdf(z) computes the area under the standard normal curve to the left of z.

Areas under the standard normal curve¶

What does scipy.stats.norm.cdf(0) evaluate to? Why?

In [28]:
normal_area(-np.inf, 0)
No description has been provided for this image
In [29]:
from scipy import stats
stats.norm.cdf(0)
Out[29]:
0.5

Areas under the standard normal curve¶

Suppose we want to find the area to the right of 2 under the standard normal curve.

In [30]:
normal_area(2, np.inf)
No description has been provided for this image

The following expression gives us the area to the left of 2.

In [31]:
stats.norm.cdf(2)
Out[31]:
0.9772498680518208
In [32]:
normal_area(-np.inf, 2)
No description has been provided for this image

However, since the total area under the standard normal curve is 1:

$$\text{area right of $2$} = 1 - (\text{area left of $2$})$$

In [33]:
1 - stats.norm.cdf(2)
Out[33]:
0.02275013194817921

Areas under the standard normal curve¶

How might we use stats.norm.cdf to compute the area between -1 and 0?

In [34]:
normal_area(-1, 0)
No description has been provided for this image

Strategy:

$$\text{area from $-1$ to $0$} = (\text{area left of $0$}) - (\text{area left of $-1$})$$

In [35]:
stats.norm.cdf(0) - stats.norm.cdf(-1)
Out[35]:
0.3413447460685429

General strategy for finding area¶

The area under a standard normal curve in the interval $[a, b]$ is

stats.norm.cdf(b) - stats.norm.cdf(a)

What can we do with this? We're about to see!

Using the normal distribution¶

Let's return to our data set of heights and weights.

In [36]:
height_and_weight
Out[36]:
Height Weight
0 73.85 241.89
1 68.78 162.31
2 74.11 212.74
... ... ...
4997 67.01 199.20
4998 71.56 185.91
4999 70.35 198.90

5000 rows × 2 columns

As we saw before, both variables are roughly normal. What benefit is there to knowing that the two distributions are roughly normal?

Standard units and the normal distribution¶

  • Key idea: The $x$-axis in a plot of the standard normal distribution is in standard units.
    • For instance, the area between -1 and 1 is the proportion of values within 1 standard deviation of the mean.
  • Suppose a distribution is (roughly) normal. Then, these are two are approximately equal:
    • The proportion of values in the distribution between $a$ and $b$.
    • The area between $a_{\: \text{(su)}}$ and $b_{\: \text{(su)}}$ under the standard normal curve.
      • Recall, $x_{i \: \text{(su)}} = \frac{x_i - \text{mean of $x$}}{\text{SD of $x$}}$.

Example: Proportion of weights between 200 and 225 pounds¶

Let's suppose, as is often the case, that we don't have access to the entire distribution of weights, but just the mean and SD.

In [37]:
weight_mean = weights.mean()
weight_mean
Out[37]:
187.0206206581932
In [38]:
weight_std = np.std(weights)
weight_std
Out[38]:
19.779176302396458

Using just this information, we can estimate the proportion of weights between 200 and 225 pounds:

  1. Convert 200 to standard units.
  2. Convert 225 to standard units.
  3. Use stats.norm.cdf to find the area between (1) and (2).
In [39]:
left = (200 - weight_mean) / weight_std
left
Out[39]:
0.656214351061435
In [40]:
right = (225 - weight_mean) / weight_std
right
Out[40]:
1.9201699181580782
In [41]:
normal_area(left, right)
No description has been provided for this image
In [42]:
approximation = stats.norm.cdf(right) - stats.norm.cdf(left)
approximation
Out[42]:
0.22842488819306406

Checking the approximation¶

Since we have access to the entire set of weights, we can compute the true proportion of weights between 200 and 225 pounds.

In [43]:
# True proportion of values between 200 and 225.
height_and_weight[
    (height_and_weight.get('Weight') >= 200) &
    (height_and_weight.get('Weight') <= 225)
].shape[0] / height_and_weight.shape[0]
Out[43]:
0.2294
In [44]:
# Approximation using the standard normal curve.
approximation
Out[44]:
0.22842488819306406

Pretty good for an approximation! 🤩

Warning: Standardization doesn't make a distribution normal!¶

Consider the distribution of delays from earlier in the lecture.

In [45]:
delays.plot(kind='hist', y='Delay', bins=np.arange(-20.5, 210, 5), density=True, ec='w', figsize=(10, 5), title='Flight Delays')
plt.xlabel('Delay (minutes)');
No description has been provided for this image

The distribution above does not look normal. It won't look normal even if we standardize it. By standardizing a distribution, all we do is move it horizontally and stretch it vertically – the shape itself doesn't change.

In [46]:
HTML('data/delay_anim.html')
Out[46]:
Your browser does not support the video tag.

Chebyshev's inequality and the normal distribution¶

  • Recall that Chebyshev's inequality states that the proportion of values within $z$ SDs of the mean is at least $1-\frac{1}{z^2}$.
    • This works for any distribution, and is a lower bound.
  • If we know that the distribution is normal, we can be even more specific!
Range All Distributions (via Chebyshev's inequality) Normal Distribution
mean $\pm \ 1$ SD $\geq 0\%$ $\approx 68\%$
mean $\pm \ 2$ SDs $\geq 75\%$ $\approx 95\%$
mean $\pm \ 3$ SDs $\geq 88.8\%$ $\approx 99.73\%$

68% of values are within 1 SD of the mean¶

Remember, the values on the $x$-axis for the standard normal curve are in standard units. So, the proportion of values within 1 SD of the mean is the area under the standard normal curve between -1 and 1.

In [47]:
normal_area(-1, 1, bars=True)
No description has been provided for this image
In [48]:
stats.norm.cdf(1) - stats.norm.cdf(-1)
Out[48]:
0.6826894921370859

This means that if a variable follows a normal distribution, approximately 68% of values will be within 1 SD of the mean.

95% of values are within 2 SDs of the mean¶

In [49]:
normal_area(-2, 2, bars=True)
No description has been provided for this image
In [50]:
stats.norm.cdf(2) - stats.norm.cdf(-2)
Out[50]:
0.9544997361036416
  • If a variable follows a normal distribution, approximately 95% of values will be within 2 SDs of the mean.
  • Consequently, 5% of values will be outside this range.
  • Since the normal curve is symmetric,
    • 2.5% of values will be more than 2 SDs above the mean, and
    • 2.5% of values will be more than 2 SDs below the mean.

Recap: Proportion of values within $z$ SDs of the mean¶

Range All Distributions (via Chebyshev's inequality) Normal Distribution
mean $\pm \ 1$ SD $\geq 0\%$ $\approx 68\%$
mean $\pm \ 2$ SDs $\geq 75\%$ $\approx 95\%$
mean $\pm \ 3$ SDs $\geq 88.8\%$ $\approx 99.73\%$

The percentages you see for normal distributions above are approximate, but are not lower bounds.

Important: They apply to all normal distributions, standardized or not. This is because all normal distributions are just stretched and shifted versions of the standard normal distribution.

Inflection points¶

  • We mentioned that the standard normal curve has inflection points at $z = \pm 1$.
    • An inflection point is where a curve goes from "opening down" 🙁 to "opening up" 🙂.
In [51]:
normal_area(-1, 1)
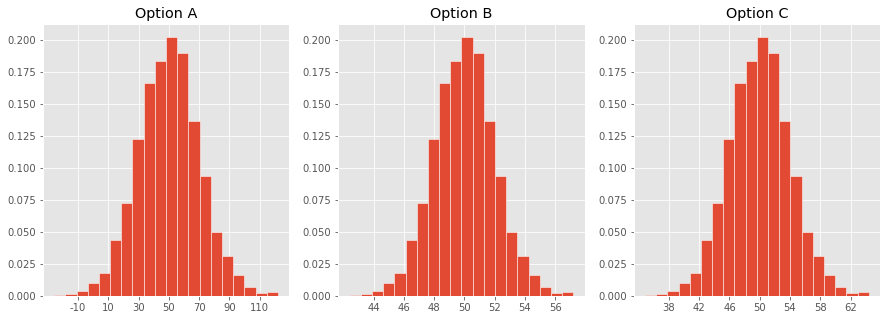
No description has been provided for this image
  • We know that the $x$-axis of the standard normal curve represents standard units, so the inflection points are at 1 standard deviation above and below the mean.
  • This means that if a distribution is roughly normal, we can determine its standard deviation by finding the distance between each inflection point and the mean.

Example: Inflection points¶

Remember: The distribution of heights is roughly normal, but it is not a standard normal distribution.

In [52]:
height_and_weight.plot(kind='hist', y='Height', density=True, ec='w', bins=40, alpha=0.8, figsize=(10, 5));
plt.xticks(np.arange(60, 78, 2));
No description has been provided for this image
  • The center appears to be around 69.
  • The inflection points appear to be around 66 and 72.
  • So, the standard deviation is roughly 72 - 69 = 3.
In [53]:
np.std(height_and_weight.get('Height'))
Out[53]:
2.863075878119538

Summary, next time¶

Summary: Spread and Chebyshev's inequality¶

  • Variance and standard deviation (SD) quantify how spread out data points are.
    • Standard deviation is the square root of variance.
    • Roughly speaking, the standard deviation describes how far values in a dataset typically are from the mean.
  • Chebyshev's inequality states that, in any numerical distribution, the proportion of values within $z$ SDs of the mean is at least $1 - \frac{1}{z^2}$.
    • The true proportion of values within $z$ SDs of the mean may be larger than $1 - \frac{1}{z^2}$, depending on the distribution, but it cannot be smaller.

Summary: Standard units and the normal distribution¶

  • To convert a value $x_i$ from a column $x$ to standard units, use $x_{i \: \text{(su)}} = \frac{x_i - \text{mean of $x$}}{\text{SD of $x$}}$.
    • A value in standard units measures the number of SDs the value is above the mean.
  • The normal distribution is bell-shaped, and arises often in nature.
  • The $x$-axis of the standard normal distribution is in standard units.
  • If we know a distribution is roughly normal, and we know its mean and SD, then we can use the standard normal distribution's curve to approximate the proportion of values within a given range without needing access to all of the data.
    • If a variable is roughly normally distributed, then approximately 68% of its values are within 1 SD of the mean, and approximately 95% of its values are within 2 SDs of the mean.

Next time¶

  • The Central Limit Theorem.
  • Confidence intervals, another way.